[BananaPancakes]

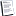
This just comes down to being familiar with the chain rule and knowing the derivatives of tan(x) and sec(x).

y' = 9 sec^2(x/3) (1/3) = 3 sec^2(x/3) = 3 [ sec(x/3) ]^2
y'' = 3 * [ 2 sec(x/3) ] sec(x/3)tan(x/3) * (1/3)
y'' = 2 sec^2(x/3)tan(x/3)

I'm fairly sure that's right.. I'm in Calculus III right now, and believe it or not, the higher level of calc you go into the simpler the derivatives/integrals get.. so it's been awhile.

Basically the chain rule is working from the outside in, multiplying the derivative of each "part".. So you have 9 tan(x/3).. Let u=x/3 if it helps.. so 9tan(u) is one "part". the derivative of 9tan(u) is 9sec^2(u).. now do the next "part", which is "u", which is x/3. the derivative of x/3 is 1/3, so you multiply 9sec^2(u) by 1/3. Get it?

Sorry, I just realized I'm not very good at explaining this.. but i'll try again.

To find the second derivative (y''), you just take the derivative of the derivative. So it's a little bit trickier as it has 3 parts this time.

the first part is.. 3 [blah]^2.. let blah= sec(x/3)
so treat blah, just like x.. and you know the derivative of 3x^2 is 6x right? But instead, we have 6(blah). now we have to differentiate blah.. which is sec(x/3).. the derivative of sec(x/3) is sec(x/3)tan(x/3)(1/3). Kinda the same as when you found the derivative.

I know it's not very clear, but I wish you knew your current understand of calc so i knew where to put more emphasis.

*there's nothing special to know about the derivative of tan(x) and sec(x).. you just have to memorize them. there's usually a list of ones to memorize on the inside of cover of most textbooks.

Edit: there's also sort of a trick to this problem. which is you need to know that sec^2(x) = [sec(x)]^2. This is true with all trig functions. sin^2(x) = [sin(x)]^2, etc.